【第34回（2020年）管理栄養士国家試験過去問解答・解説】問193-194応用力試験「県の行政栄養士による栄養調査」

【解説】
1＝○：調査日数を増やして誤差を小さくできるのは、日間変動であるため、正しい記述です。

日間変動とは、日によって食事内容などが異なる変動のことです。

例えば、食事調査の前日に調査対象者がたまたま食べ放題に行っていたら、翌日の食事調査では食べ放題での食事摂取状況を反映した値となります。

統計学的にはこのような異常な値は「外れ値」といい、外れ値を含んだすべての値を均したものが平均値、外れ値を除外して均したものが中央値といいます。

こういった個人がその日ごとに行う行動の変化を個人内変動といいますが、このような特殊な状況の値は、その人の日常的な姿を反映している値とはいえませんし、このような値を含むことで、本来的な値から乖離させる誤差を生むことになります。

そのため、調査日に平均的な日常を多く含むことで、よりその人の実態を反映した値を得ることができます。

したがって、日間変動などの個人内変動がある要因については調査日を増やすことで、誤差を小さくすることができます。

2＝×：季節間変動による誤差は調査日数を数日増やしても修正できないため、誤った選択肢です。

季節間変動とは、季節の影響を受けることで生じる変動です。

例えば、冬はみかんを食べる人が多いかと思いますし、逆に春はそんなにみかんや果物を食べないかもしれません。
夏場は暑くてお米を食べるほど食欲がないので、そうめん中心の食事の人もいるかもしれません。

このように季節に影響を受けて食事内容が変わることを、季節間変動があるといいます。

調査日を数日程度増やして延長したところで季節は変わらないので、季節間変動による誤差の縮小は望めません。

3＝×：過小申告による誤差は調査日数を数日増やしても修正できないため、誤った選択肢です。

過少申告とは、対象者が調査において自身の値を実際より過少に申告することです。

例えば、太っている人が、食事量をごまかそうと、少な目に調査で回答するようなことです。

調査日を数日程度増やして延長したところで、調査対象者が過少に申告しようという気持ちには影響がほとんどないと考えられるため、誤りです。

4＝×：過大申告による誤差は調査日数を数日増やしても修正できないため、誤った選択肢です。

過大申告とは、対象者が調査において自身の値を実際より過大に申告することです。

例えば運動不足の人が、運動していると見せかけようと、運動量・回数を多めに調査で回答するようなことです。

調査日を数日程度増やして延長したところで、調査対象者が過大に申告しようという気持ちには影響がほとんどないと考えられるため、誤りです。

【解説】
集団の統計を考えた時、集団の実態を反映する真の値は、極端な外れ値（両側の値）が少なくなり、集団の構成人数が多いところの値（最頻値）は高くなると考えられるため、正規分布曲線グラフの山は極度に高くなる形となります。

しかし、実際の測定値はさまざまなバイアス（偏り）により外れ値も多く含むため、集団の構成人数が多いところの値（最頻値）は真の値より低く、分布曲線グラフの両端は高くなります。したがって、実際の測定値は真の平均値を含むグラフよりなだらかな山を描きます。

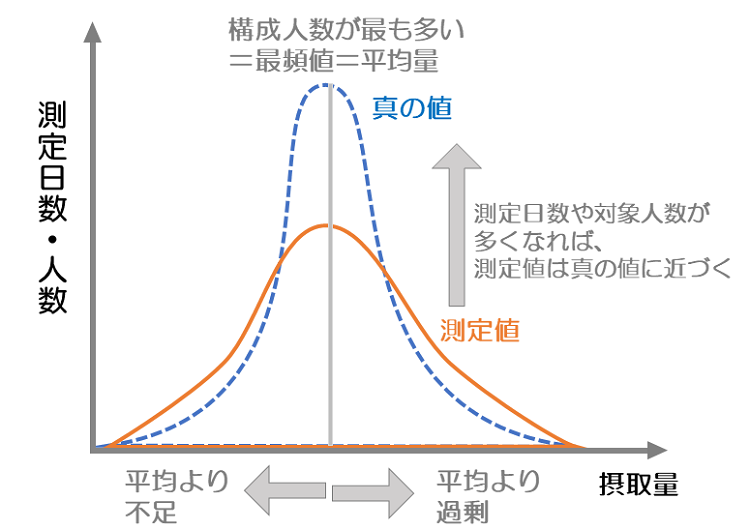
1・3＝×：1日調査よりも3日調査のほうが調査日数が多くて日間変動のバイアス（偏り）が少なく、統計として精度が高い＝真の値に近いと考えられますから、上の図でいえば、測定値（精度が低い値）が1日調査、真の値（精度が高い値）が3日調査と読み替えることができます。

そのように考えると、測定の日数や人数が増えても、摂取量の平均値自体は差がないことがわかります。

したがって、平均値の変動を述べている選択肢（1）や（3）は除外されます。

2＝×：1日調査よりも精度が高い3日調査では、外れ値をとる（不足・過剰を示す）人数が少なくなり、不足している者の人数の割合は低くなるため、誤った選択肢です。

4＝○：測定日数や対象人数が多くなれば、測定値は真の値に近づくため、調査日数が増えれば、食塩摂取量が目標量を超えている者の割合も高くなると考えられ、最も適切な選択肢です。